准确描述材料的损伤和断裂行为对预防材料失效、保障结构安全具有重要意义。基于连续介质力学的损伤方法，又称“弥散断裂方法”，通过在损伤区引入局部化的损伤变量，实现了对裂纹萌生与扩展的统一建模。然而，传统的局部损伤模型的数值解存在网格依赖性。Bažant等人指出，基于局部损伤参数的软化行为导致了控制方程的不适定性，在准静态分析中失去了椭圆性，在动态分析中失去了双曲性。针对这一问题，Peerlings等人通过引入梯度增强项，发展出非局部的梯度损伤模型，实现了控制方程的正则化，避免了数值解的网格依赖性。但传统梯度损伤模型依然存在两大理论缺陷，即难以保证损伤演化过程的收敛性和单调性。
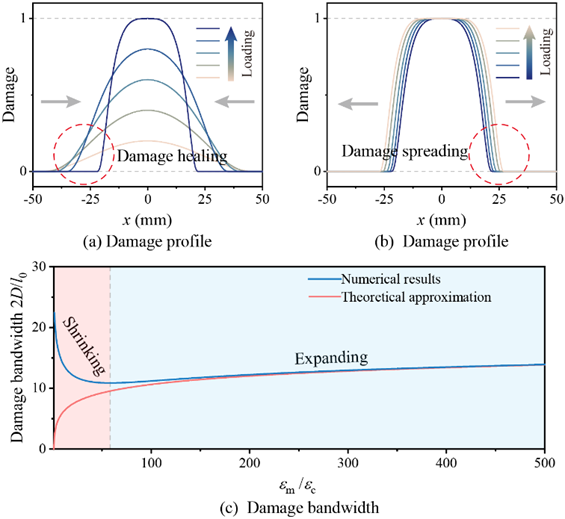
首先，损伤形貌缺乏收敛性。大量研究表明，梯度损伤模型在加载过程中会发生损伤的非物理性扩散，即损伤区域随加载持续扩宽而不是局部化为宏观裂纹。Geers和de Borst等学者尝试引入随损伤程度演化的非局部相互作用来减缓损伤的非物理性扩散，但这些方法往往是基于经验的现象学修正，缺乏严格的理论依据，尚未形成通用的收敛性控制机制。
其次，损伤演化的不可逆性难以自然实现。不可逆性是热力学第二定律对损伤耗散过程的基本要求，但在传统梯度损伤模型中，损伤变量在无特殊处理时可能出现自愈现象，通常需要采用驱动力或者损伤变量的历史最大值来强制满足损伤演化的单调性。Marigo等人指出，这种人为强制的不可逆性会使得实际损伤形貌和力学响应偏离理论预期，影响模型可靠性。
总之，传统梯度损伤模型在收敛性与单调性方面存在的根本性问题，严重制约了其物理一致性与工程适用性，而现有研究仅在特定场景或特定假设下对这些问题进行有限处理。因此，构建一种严格满足收敛性与不可逆性的梯度损伤模型框架，成为当前损伤力学领域亟需突破的关键问题。
图1：传统梯度损伤模型中的损伤愈合和非物理性损伤扩散现象
针对上述难题，中国科学技术大学计算力学实验室提出了一种严格满足损伤演化收敛性和单调性条件的改进梯度损伤模型。在此基础上，模型通过求解第一类Volterra积分方程，实现了任意形式内聚律的自然引入，从而可以广泛描述不同准脆性材料的损伤和断裂行为。
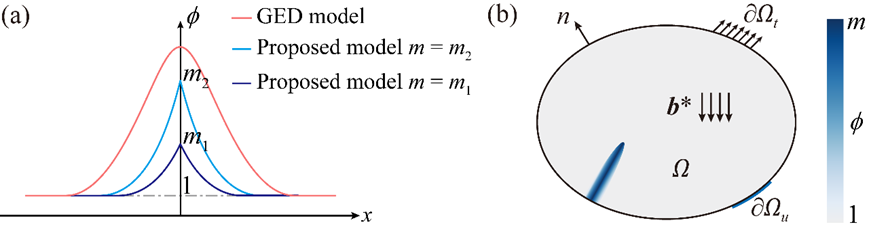
首先，本研究推导了传统梯度损伤模型的损伤带宽理论解。该理论解表明，传统非局部损伤模型出现非物理性损伤扩散的根本原因在于非局部变量的无界性。损伤区域随着非局部变量的增大无限扩宽，从而导致损伤的非物理性扩散。为此，本研究引入了显式收敛机制，通过在梯度损伤模型的驱动项中引入退化函数，使得驱动力在非局部变量演化到达m时自然衰减，进而将非局部变量严格约束在[1, m]范围内，实现对损伤带宽的显式“锁定”与收敛，并且可以通过改变非局部变量的上界m来改变损伤形貌，无需修改损伤形貌函数。
图2：具有收敛可变上限的梯度损伤模型
其次，本研究发现保证损伤不可逆性的关键在于损伤形貌和内聚律的解耦。现有文献中，能保证损伤不可逆性的梯度损伤模型通常仅适用于理想脆性材料，而通过引入各类内聚律以描述不同材料软化行为的模型往往不能自然满足损伤不可逆性，这种损伤不可逆性和软化行为泛用性的冲突造成了一种“鱼与熊掌不可兼得“的局面。为此，本研究在能量耗散机制中引入额外耗散项，在理论上实现了损伤演化过程与内聚律之间的显式解耦。具体而言，研究通过构造合适的损伤形貌函数α(ϕ)和残余强度函数β(ϕ)，保证了损伤变量在加载过程中严格单调递增。此外，为实现模型等效内聚律与目标内聚律之间的一致性，研究进一步建立了关于刚度退化函数g(ϕ)的第一类Volterra积分方程，在不预设α(ϕ)和β(ϕ)具体形式的前提下，导出了g(ϕ)的一般表达式。这一框架不但保证了损伤演化的不可逆性，而且实现了对任意形式内聚律的自然兼容。
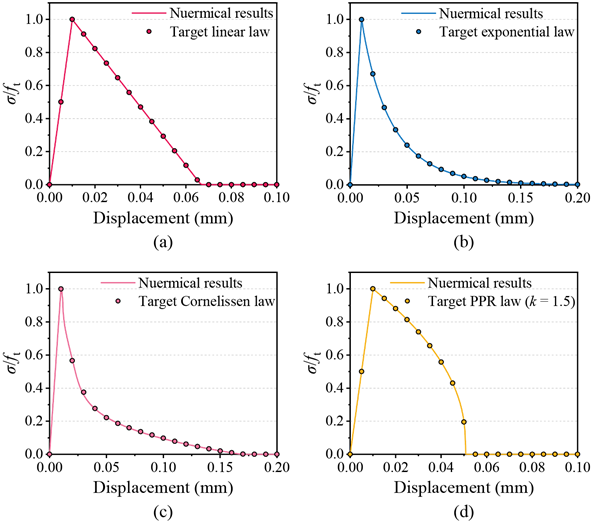
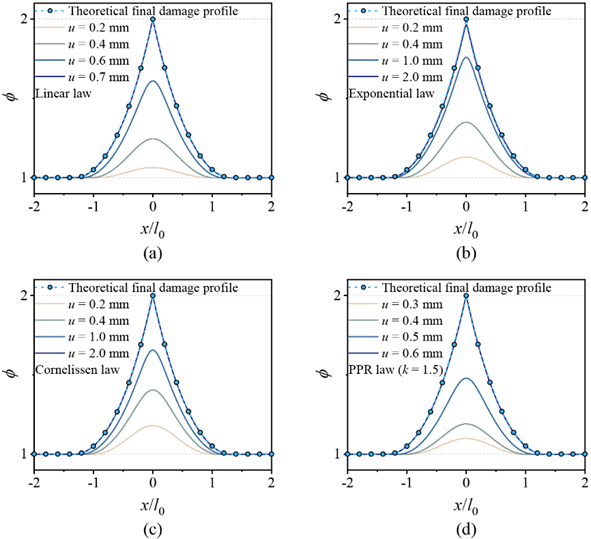
通过一维杆的拉伸破坏算例，研究证明了模型对任意内聚律的兼容性。如图3所示，无论是在凸函数形式还是凹函数形式的内聚律情况下，模型的力学响应都与理论预期值一致，并且损伤演化过程都严格满足单调性和收敛性条件（图4）。图3：模型在不同内聚律情况下的力位移响应曲线
图4：不同内聚律情况下的损伤演化过程
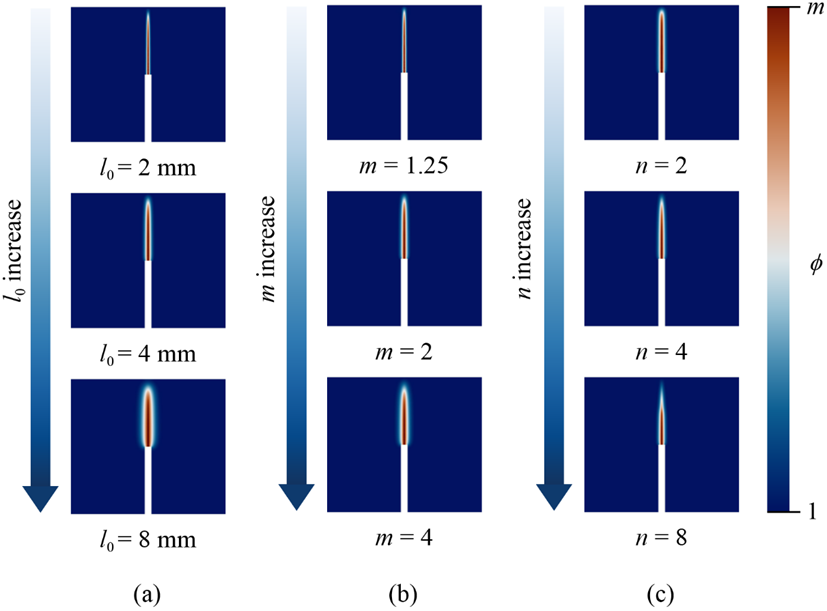
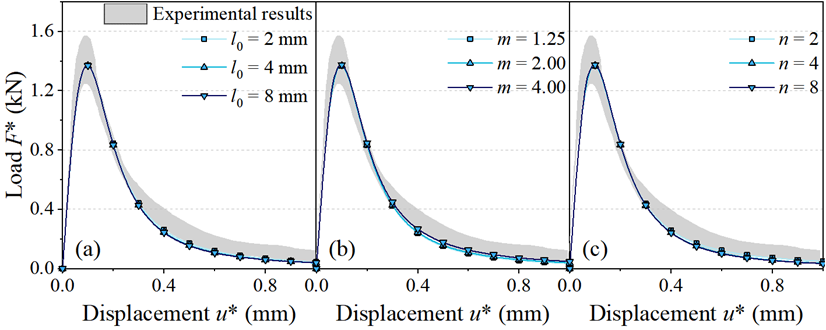
本研究在不同的参数情况下进行了混凝土梁三点弯曲的数值模拟。结果表面，模型的长度尺度l0，非局部变量的上界m，以及残余强度函数的指数n，只会影响损伤相貌，不会对模型的力学响应造成显著影响，如图5，6所示。研究结果同时还体现了模型的双重𝛤收敛性，当长度尺度l0→0或非局部变量的上界m→1时，损伤带宽趋于0，同时模型的力学响应严格遵循目标内聚律。由此证明，模型在极限情况下可收敛至经典的离散内聚力模型（cohesive zone model），在理论与数值层面实现了与断裂力学基本原理的一致性。
图5：混凝土三点弯模拟中不同参数情况下的损伤形貌
图6：混凝土三点弯模拟中不同参数情况下的力-位移响应曲线
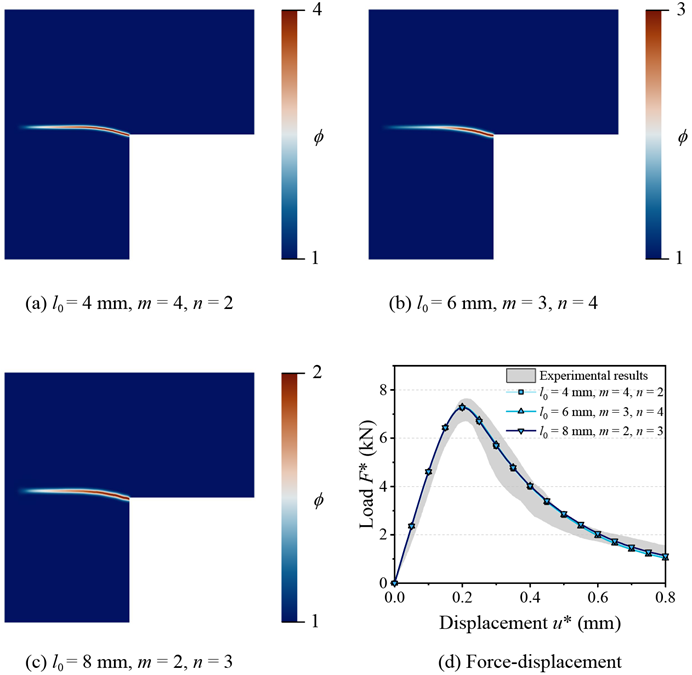
该模型进一步被用于模拟L型板的混合模式破坏过程，在三组不同的模型参数组合下（l0, m, n）下开展了系统的数值计算，模拟所得到的力-位移响应与实验结果高度一致。尽管参数的变化影响了最终损伤形貌，但对整体力学响应无明显影响，表明模型在混合模式破坏分析中具有良好的参数不敏感性和物理可预测性。
图7：L型板混合模式破坏模拟中的损伤形貌和力-位移响应曲线
本研究建立了一种新的梯度损伤模型框架，在理论上严格满足了损伤演化过程的收敛性与单调性要求，并通过求解第一类Volterra积分方程引入了任意形式的内聚律，在不依赖预设特定函数形式的前提下实现了对任意形式内聚律的自然嵌入，从而具备广泛描述不同材料软化行为的能力。此外，模型还表现出双重𝛤收敛性，并且其整体力学响应对参数选择不敏感，具备良好的稳定性与物理一致性，为准确描述材料的失效行为提供了严格的理论支持。研究成果以“A rigorously convergent and irreversible gradient damage model”为题，发表于《Journal of the Mechanics and Physics of Solids》期刊，计算力学实验室博士研究生黄含伟为论文第一作者，该研究得到了国家自然科学基金基础科学中心、国家双一流建设经费、中央高校基本业务经费等资助。原文链接：
https://doi.org/10.1016/j.jmps.2025.106262
实验室概况
相关新闻