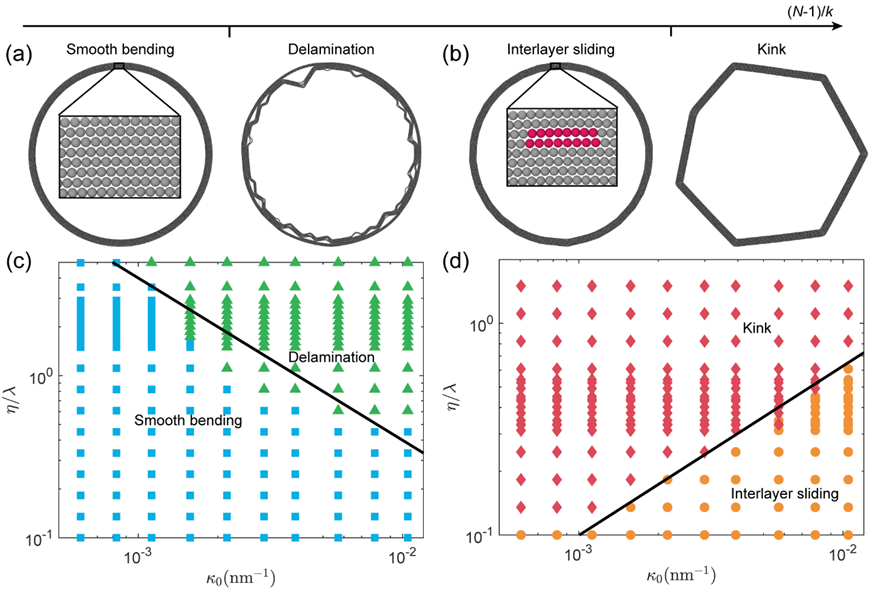
多层范德华材料（石墨烯、六方氮化硼、过渡金属硫族化合物等）正在重塑先进材料与器件工程。其兼具卓越的电子、光学、热学与力学性能，已成为下一代功能器件的核心平台。这类材料层内强共价键—层间弱范德华作用的独特结构，使其弯曲行为呈现高度敏感性与可编程特征，如平滑弯曲、层间滑移、局部分层/波纹化（Ripplocation）到扭结（Kink）等典型形貌（图1），从而能够直接调控器件稳定性与材料极限变形能力。在此，弯曲是性能演化的主导机制，例如多层石墨烯弯曲中出现的 超软化现象，即源于层间滑移逐步主导响应。弯曲—形貌耦合效应具有跨尺度普适性，例如通过在块体氮化硼中引入扭转堆垛纳米片层，可在室温下协同实现高强度与高塑性，其核心机制正是分层、波纹化与扭结等形貌的有序演化。此类进展印证了层间相互作用工程化对优化层状材料性能的关键作用，并凸显建立普适理论框架的迫切性。
图1：多层范德华材料弯曲典型形貌及其模型示意图。从左到右分别为平滑弯曲、局部分层、层间滑移和扭结
然而，现有理论仍存在关键局限：（1）模型普适性不足。传统降维模型依赖强边界假设或忽略层内弹性，难以统一描述滑移—分层—扭结全序列演化；（2）控制参数缺失。层间滑移与曲率局域化缺乏可量化、跨场景映射的统摄参数，严重制约形貌转化预测能力。直接后果是：不同实验测得的有效弯曲刚度难以互证，工程领域更亟需参数—形貌—性能可检索图谱指导精准设计。
针对上述挑战，中国科学技术大学近代力学系计算力学实验室团队联合清华大学高华健教授，提出了普适弹性线新框架。该框架在一个统一模型中同时纳入几何非线性、层内弹性变形与层间相对滑移，并引入两个关键无量纲参数：剪滞系数（Shear-lag coefficient, k），表征层间滑移耦合强度；弯剪系数（Shear-bending coefficient, η），量化局部曲率局域化程度。基于此框架，研究团队取得以下核心成果：
图2：静态模态弯曲刚度随层数N、剪滞系数k和外载特征cm的变化
提出静态模态弯曲刚度Dm：通过模态分解定义静态模态弯曲刚度 (Dm)。该参数系统揭示多层范德华材料弯曲刚度随外加载荷特征变化的规律，从根本上解释不同实验方法测量有效刚度存在差异的根源。Dm的关键价值在于解耦材料本征弯曲响应与实验边界条件，确立其作为多层范德华材料弯曲刚度本征特征的地位。研究精准量化Dm随结构尺寸变化的标度律。该结果区分了材料本征响应与外加载荷/约束的耦合，将传统弯曲刚度测量值重新诠释为模态分量的权重叠加，解决了不同实验方法间长期存在的测量不一致性难题（图2）。
构建形貌图谱：系统揭示了多层范德华材料弯曲的四种典型形貌（平滑弯曲、层间滑移、局部分层、扭结）的出现条件及其相互转变路径。基于剪滞系数（k）与弯剪系数（η）构成的参数空间，绘制直观的形貌图谱，为工程设计提供直接参考（图3）。
提出可变形性因子Ξ*：定义了一个可调控的无量纲参数——可变形性因子（Ξ*）。该因子综合了层数、单层弯曲刚度、层间相互作用强度等核心参数的影响。Ξ*的核心功能在于定量评估范德华材料在弯曲过程中更倾向于发生哪种主导行为：当Ξ*较大时，材料倾向于发生滑移塑化，有利于实现更大的可变形性；当Ξ*较小时，材料则更易发生分层或扭结失稳，显著削弱其承载能力。Ξ*为材料可变形性的设计提供了直接的量化标度（图4）。
图3：平均曲率下多层范德华材料形貌在剪滞系数k和弯剪系数η空间的图谱
核心发现与机制解析
该研究取得以下关键发现（图3和图5）：
形貌主导机制判据：层间相对运动受限时（高剪滞系数），以平滑弯曲为主；层间易滑移时（低剪滞系数），出现滑移主导的可塑化过程；当局部压缩累积则引发局部分层；而在各层充分解耦时，即使平均曲率不大，也可能形成扭结。这四种形貌在无量纲参数空间中呈现有序转换。
扭结触发路径：扭结形成的关键在于局域曲率集中（高弯剪系数），而非极大的整体弯曲。局部微小分层导致层内应变能快速释放，进而自发转化为稳定的扭结，并伴随承载能力突降。
滑移与分层的竞争机制：团队给出先滑移还是先分层的定量判据：当剪滞系数较低且弯剪系数较小时，滑移更易发生；弯剪系数较大时，分层阈值更低。模拟结果验证了该判据可靠性。
尺寸与材料参数效应：层数多、单层弯曲刚度高的范德华材料更易发生分层或扭结；层数少、单层弯曲刚度低、层间剪切作用弱的体系则倾向于“滑移塑化”，可变形能力更强。这些规律与多层范德华材料体系的独立实验观察吻合。
图4：多层范德华材料无量纲可变形因子（左图）以及层数影响（右图）
模型验证与设计原则
1 . 模型验证：
通过粗粒化分子动力学模拟多层悬臂梁的集中加载情况，载荷—位移响应与形貌演化与理论预测高度一致。模拟清晰捕捉四种响应（图6）：
弹性主导区：载荷—位移近似线性关系，层间堆垛稳定。
分层主导区：超过阈值后载荷显著下降，局部形貌演化为波纹化。
扭结主导区：微小位移下形成扭结对，载荷骤降至接近零并伴随波动。
滑移主导区：载荷—位移曲线呈现“平台—波动”的类塑性特征。
上述响应与理论形貌图谱分区一一对应。边界条件主要影响局部变形分布，但不改变形貌判据本身（如分层与扭结更易在弯矩集中区域发生）。
图5：层数固定（N=31）条件下弯曲形貌在参数空间中的分布规律
图6：层数固定（N=31）条件下，载荷强度与材料参数空间对弯曲响应与形态分化的调控
2 . 设计原则：
结合模型预测、模拟验证以及对关键实验现象的解释力，研究提出以下关键材料与结构设计指引：
提升可变形性（促进滑移塑化，抑制扭结失稳）：优先采用较少层数结构、降低层间滑移能、提高单层弯曲刚度。此策略（对应增大Ξ*）有助于促进层间滑移耗能机制，有效抑制早期分层与扭结失稳，实现更大的可变形能力。例如，扭转堆垛层状氮化硼陶瓷在室温下实现高强度—高塑性组合的成功案例（Nature, 2024, 626, 779-784），其内在机制与本模型揭示的规律高度一致，即通过优化层间堆垛（降低层间滑移能）和抑制曲率局域化效应来实现。本工作提出的可变形性因子 Ξ*为该现象提供了定量解释框架（图4）。
本研究为理解多层范德华材料弯曲中层内—层间—几何非线性耦合这一核心问题提供了简洁而普适的解决方案：以两个无量纲参数整合关键物理因素；用形貌图谱将复杂演化关系可视化；借可变形性因子Ξ*量化工程关切的强度—塑性—形貌指标。该框架为柔性电子、微纳器件及层状陶瓷等领域提供了新的设计视角，使得在器件设计初期预判材料在目标载荷下的形貌与承载响应成为可能，有望降低试错成本，推动性能优化进程。研究成果以“Generalized Elastica Theory for Multilayered van der Waals Materials: Morphological Transformations and Deformability”为题发表于《Journal of the Mechanics and Physics of Solids》。本文第一作者为中国科学技术大学优秀博士毕业生、现新加坡南洋理工大学博士后何泽洲，通讯作者为中国科学技术大学吴恒安教授与清华大学高华健教授。该研究得到了国家自然科学基金基础科学中心、国家双一流建设经费、中央高校基本业务经费等资助。
原文链接：https://doi.org/10.1016/j.jmps.2025.106320
实验室概况
相关新闻